Capítulo 5 Modelos con respuesta normal

En este capítulo se describirán los métodos y modelos estadísticos para analizar medidas respetidas cuando la variable respuesta sigue una distribución normal o gaussiana. Se pueden probar algunas transformaciones, como el logaritmo, para normalizar la distribución de la variable.

5.1 Técnica de la suma de cuadrados

Este método o técnica se basa en la suma de cuadrados. Es la más simple desde el punto de vista estadístico y computacional. Por contra, sólo permite analizar diseños balanceados, sin variables independientes cuantitativas (covariables), sólo cualitativas o factores y con un número limitado de factores que tienen que estar cruzados (no anidados). A continuación se presentan los dos diseños más simples de medidas repetidas que se pueden analizar con esta técnica.

5.1.1 Diseño 1W+1B

Cuando el diseño es balanceado (mismo número de individuos por grupo), las medidas son las mismas para todos los individuos y no hay covariables, se puede usar la técnica de suma de cuadrados o tabla ANOVA.

La notación que se usa para la ecuación del modelo en el contexto de suma de cuadrados es:

\[y_{ijk} = \mu + \alpha_i + \beta_j + \alpha\beta_{ij} + \pi_{k(i)} + e_{ijk}\]

Donde

\(\mu\) es la constante del modelo,
\(\alpha_i\), son los efectos del grupo o tratamiento
\(\beta_j\), son los efectos del tiempo
\(\alpha\beta_{ij}\) es la interacción del tiempo con el grupo
\(\pi_{k(i)}\) es el efecto aleatorio del individuo que está anidado al grupo
\(e_{ijk}\) son los errores

\(\sum_{i=1}^a \alpha_i=0\), \(\sum_{j=1}^b \beta_j=0\), \(\sum_{i=1}^a \alpha\beta_{ij}=0, \forall j\), \(\sum_{j=1}^b \alpha\beta_{ij}=0, \forall i\),

\(\pi_{k(i)} \sim N(0, \sigma_{ind})\) \(e_{ijk} \sim N(0, \sigma)\) indep

En este contexto se dice que el tiempo y la interacción tratamiento:tiempo son términos o componentes “intra sujeto” (within subject). Mientras que el grupo es un componente “entre sujeto” (between subject). Por lo tanto, se trata de un diseño 1W+1B.

Las técnicas clásicas de la tabla ANOVA y su inferencia són válidas siempre y cuando se cumpla la condición de esfericidad: la variancia de la diferencia entre dos medidas es constante. Para comprobar la condición de esfericidad se puede aplicar el test de Mauchly.

Si no se cumple hay que corregir los grados de libertad de los términos “intra sujetos” de la tabla ANOVA y se recalculan sus p-valores. Hay dos métodos para corregir los grados de libertad: método “Huynh and Feldt” (H-F) y el método “Greenhouse-Geisser” (G-G) .

5.1.2 Diseño 1W

Si en el diseño no hay grupos, luego el modelo se simplifica a un diseño de un solo factor “intra sujeto” (1W)

\[y_{ij} = \mu + \pi_i + \beta_j + e_{ij}\]

En ambos casos, tanto en el diseño en que tenemos grupos (1W+1B) como en el que no (1W), no nos interesa evaluar el efecto del individuo; ya sabemos que hay variabilidad entre ellos. Veremos en un ejemplo como el paquete ez que se usará para esta técnica de suma de cuadrados omite los resultados sobre el factor aleatorio individuo.

5.1.3 Función `ezANOVA`

Para ajustar los modelos de medidas repetidas balanceados mediante la técnica de suma de cuadrados existe la función ezANOVA del paquete ez.

library(ez)

Tanto la corrección por H-F o G-G, como el test de esfericidad de Mauchly estan implementados en el package ez de R. Para visualizar gráficamente los resultados, se usará la función ezPlot(). Más adelante en esta sección se verá en un ejemplo de ambas funciones. Para llevar a cabo los análisis ANOVA se usa la función ezANOVA () que tiene los siguientes argumentos:

data: base de datos donde se encuentran las variables
dv: variable respuesta o variable dependiente
wid: variable individuo
within: factor o factores “intra sujeto”. Típicamente en este argumento se espedificará el tiempo. Si se especifica más de un factor, éstos deben estar cruzados y se escribirá .(var1,var2).
between: factor o factores “entre sujetos”. Si no hay ningún factor “intra-sujeto” se deja a NULL. Como en el argumento within, si hay más de un factor “entre sujetos”, éstos deben estar cruzados y se escribirá .(var1,var2).

Observaciones:

Los datos deben estar en formato vertical.
La variable respuesta y los factores deben escribirse sin comillas.
Los factores “intra”, “entre” y el sujeto deben estar en format factor.
El factor individuo debe tener tantos niveles como individuos.
Aunque en teoría la función permite covariables (variables independientes contínuas), esta opción está en versión “beta”.
Todos los factores, excepto el individuo, deben ser de efectos fijos.

5.2 Respuesta Multivariante

Esta metodología también conocida como MANOVA asume que las observaciones de cada individuo es un vector multivariante donde la variable respuesta se considera dicho vector. Podemos escribirlo de la siguiente forma:

\[\vec{y}_i = \vec{\mu}_i + \vec{e}_i\]

Donde

\(\vec{y_i}=(y_{i1},\ldots,y_{iT})\) es el vector de medidas para el individuo \(i\).
\(\vec{\mu}_i=(\mu_{i1},\ldots,\mu_{iT})\) es el vector con las medias de cada momento y para cada individuo. Las medias pueden depender de las variables independientes \(x_k\). Fíjate que el coeficiente \(\beta_{kj}\) puede ser diferente para cada momento.

\[\mu_{ij} = \sum_{k=1}^K \beta_{jk} x_{ik}, \quad j=1,...,T\]

\(\vec{e_i} \sim N(\vec{0},\Sigma)\), donde \(\Sigma\) es la matrix de covarianzas de los errores y tiene que ser la misma para todos los individuos. Su estructura, pero, puede ser cualquiera.
\(x_{ik}\) valor de la variable independiente \(k\) del individuo \(i\).

Observaciones

Para ajustar este modelo los datos se disponen de forma horizontal (ancho).
En este modelo los tiempos en que se toman las \(T\) medidas tienen que ser los mismos para todos los individuos.
Para estudiar la evolución en el tiempo se puede realizar un contraste polinómico en el vector de medias \(\vec{\mu}\).
Para comparar grupos de medidas, por ejemplo si se tienen cinco medidas, las dos primeras corresponden al tratamiento A y las otras tres al tratamiento B, se puede realizar un contraste lineal para comparar los dos tratamientos.
Cuando hay un valor faltante en alguna medida, toda la fila del individuo se tiene que eliminar.
Cada variable independiente, \(x_{ki}\) es un único valor por individuo. O sea, que este modelo no contempla que las variables independientes sean de medidas repetidas. Si tuviéramos una variable que cambiara en el tiempo, se tienen que poner como variables diferentes (una para cada momento).
Los factores contribuyen con tantas dummy variables como categorías menos uno en los términos \(x_{ik}\).
Los términos \(x_{ik}\) pueden ser también interacciones entre variables, como el producto de sus términos.

Datos				Matriz de diseño `~ fumador + edad + sexo + edad:fumador`
indiv	edad	fumador	sexo	fumadorEx	fumadorNunca	edad	sexomujer	fumadorEx:edad	fumadorNunca:edad
1	50	Ex	mujer	1	0	50	1	50	0
2	55	Actual	mujer	0	0	55	1	0	0
3	60	Actual	hombre	0	0	60	0	0	0
4	65	Nunca	mujer	0	1	65	1	0	65
5	62	Ex	hombre	1	0	62	0	62	0

5.3 Ejemplos

Vamos a ver algunos ejemplos que se analizarán mediante las técnicas que se acaban de describir.

5.3.1 Ejemplo 1

En la base de datos “Ejemplo_1W.csv” se tienen los datos de un diseño con 12 individuos en los que se toman los niveles en sangre de un cierto parámetro lipídico. Para cada invidivuo se miden los niveles a 1, 2 y 3 horas.

datos <- read.csv2("datos/Ejemplo_1W.csv")

Ordenamos por individuo y dentro por tiempo dentro de individuo

datos <- arrange(datos, indiv, tiempo)

5.3.1.1 Exploración de los datos

library(ggplot2)
p <- ggplot(data = datos, aes(x = tiempo, y = medida, group = indiv))
p + geom_line(col="grey") + stat_summary(aes(group = 1),
    geom = "line", fun = mean, size=2)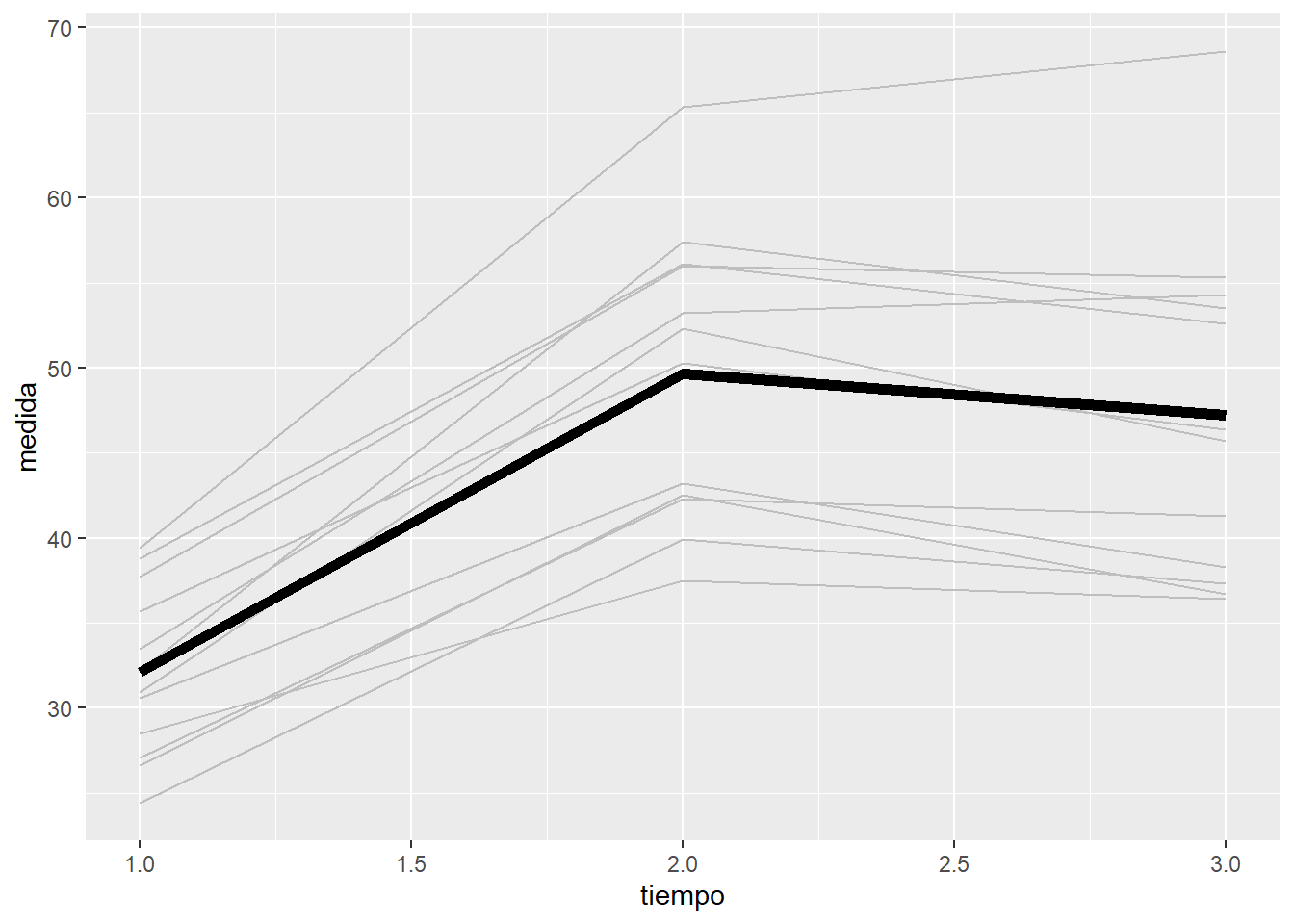

Cada línea representa a un individuo, mientras que la línea más gruesa es el promedio de los 12 individuos. Vemos como el efecto del tiempo no es del todo lineal. Además las líneas están bastante separadas indicando variabilidad entre los individuos.

Comprobemos si tenemos algún inviduo con datos faltantes

sum(with(datos, tapply(is.na(medida), indiv, any)))

[1] 0

Como son datos balanceados, podemos usar ANOVA y MANOVA

5.3.1.2 Suma de cuadrados (ANOVA)

Para ajustar este modelo hay que usar los datos en disposición vertical. Además, hay que convertir las variables tiempo e indiv a factor.

library(ez)

datos.ez <- datos
datos.ez$tiempo <- factor(datos.ez$tiempo)
datos.ez$indiv <- factor(datos.ez$indiv)

ezANOVA(data=datos.ez, dv=medida, wid=indiv, within=tiempo, detailed = TRUE)

$ANOVA
       Effect DFn DFd       SSn       SSd         F            p
1 (Intercept)   1  11 66546.801 1892.0589 386.88796 6.390053e-10
2      tiempo   2  22  2166.376  264.6244  90.05264 2.542699e-11
  p<.05       ges
1     * 0.9686088
2     * 0.5011210

$`Mauchly's Test for Sphericity`
  Effect         W          p p<.05
2 tiempo 0.4433135 0.01712201     *

$`Sphericity Corrections`
  Effect       GGe        p[GG] p[GG]<.05       HFe        p[HF]
2 tiempo 0.6423901 5.662497e-08         * 0.6905331 1.998401e-08
  p[HF]<.05
2         *

La condición de esfericidad no se cumple dado que el test de Mauchly es significativo. Por lo tanto, hay que corregir los grados de libertad y, en consecuencia, el p-valor del factor tiempo. Después de la corrección, éste sigue siendo significativo.

5.3.1.3 Modelo de respuesta multivariante (MANOVA)

Para analizar los datos mediante el modelo de respuesta multivariante hay que disponer los datos de forma horizontal.

datosh <- dcast(datos, indiv ~ paste0("medida_", tiempo),
                 value.var = "medida" )
datosh

   indiv medida_1 medida_2 medida_3
1      1     39.4     65.3     68.6
2      2     33.5     53.2     54.3
3      3     27.1     42.3     41.3
4      4     30.9     52.3     45.7
5      5     32.2     57.4     53.5
6      6     26.6     42.5     36.7
7      7     28.5     37.5     36.4
8      8     37.7     56.0     55.3
9      9     35.7     50.3     46.4
10    10     30.6     43.2     38.3
11    11     24.4     39.9     37.3
12    12     38.8     56.1     52.6

Para ajustar un modelo de regresión lineal con respuesta multivariante se puede usar la función lm. Y hay que poner la variable respuesta a la izquierda de ~ como una matriz de las tres variables (medida.1, medida.2 y medida.3):

respuesta <- as.matrix(datosh[,c("medida_1","medida_2","medida_3")])
modelo <- lm(respuesta ~ 1, data=datosh)
class(modelo)

[1] "mlm" "lm"

summary(modelo)

Response medida_1 :

Call:
lm(formula = medida_1 ~ 1, data = datosh)

Residuals:
    Min      1Q  Median      3Q     Max 
-7.7167 -3.9667 -0.5667  4.0833  7.2833 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   32.117      1.445   22.23 1.72e-10 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5.006 on 11 degrees of freedom


Response medida_2 :

Call:
lm(formula = medida_2 ~ 1, data = datosh)

Residuals:
    Min      1Q  Median      3Q     Max 
-12.167  -7.217   1.633   6.358  15.633 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   49.667      2.456   20.22 4.75e-10 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 8.509 on 11 degrees of freedom


Response medida_3 :

Call:
lm(formula = medida_3 ~ 1, data = datosh)

Residuals:
   Min     1Q Median     3Q    Max 
-10.80  -9.15  -1.15   6.50  21.40 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   47.200      2.867   16.47 4.25e-09 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 9.93 on 11 degrees of freedom

Para obtener la matriz de covarianzas de los residuos:

estVar(modelo)

         medida_1 medida_2 medida_3
medida_1 25.05970 36.58970 42.08727
medida_2 36.58970 72.39879 81.30000
medida_3 42.08727 81.30000 98.60364

Y a partir de la matriz de covarianzas, se puede calcular fácilmente la matriz de correlaciones de los residuos:

cov2cor(estVar(modelo))

          medida_1  medida_2  medida_3
medida_1 1.0000000 0.8590239 0.8466744
medida_2 0.8590239 1.0000000 0.9622290
medida_3 0.8466744 0.9622290 1.0000000

Para obtener los resultados se usa la función anova (?anova.mlm)

anova(modelo, X = ~1, test = "Pillai")

Analysis of Variance Table


Contrasts orthogonal to
~1

            Df Pillai approx F num Df den Df    Pr(>F)    
(Intercept)  1  0.945   85.903      2     10 5.035e-07 ***
Residuals   11                                            
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Los estadísticos disponibles (argumento test) son: “Pillai”, “Wilks”, “Hotelling-Lawley”, “Roy” o “Spherical”.

Con la opcion X=~1 se contrasta si \(\mu_1 = \mu_2 = \mu_3\). En cambio la opción por defecto X = ~ 0, contrasta \(\mu_1 = \mu_2 = \mu_3=0\) que no es de interés.

El término (Intercept) corresponde al efecto del tiempo.

Resultado

Hay efecto del tiempo porque el p-valor < 0.05.

5.3.2 Ejemplo 2

En la base de datos “Ejemplo_1W1B.csv” se tienen los datos de un estudio en el que participan 24 individuos randomizados en dos grupos de tratamiento (trat). Como en el anterior ejemplo, para cada invidivuo se miden los niveles a 1, 2 y 3 horas.

datos <- read.csv2("datos/Ejemplo_1W1B.csv")

Como antes, ordenamos por individuo (de 1 a 24) y por tiempo

datos <- arrange(datos, indiv2, tiempo)

Fíjate que hay dos variables que codifican al individuo: la variable indiv va de 1 a 12 que son los individuos que hay dentro de cada grupo de tratamiento, mientras que indiv2 va de 1 a 24 que son el total de individuos.

5.3.2.1 Exploración de los datos

datos$trat <- factor(datos$trat, 1:2, c("Control","Tratados"))

library(ggplot2)
p <- ggplot(data = datos, aes(x = tiempo, y = medida, group = indiv2))
p <- p + geom_line(col="grey") + stat_summary(aes(group = 1),
    geom = "line", fun = mean, size=2)
p + facet_grid( ~ trat)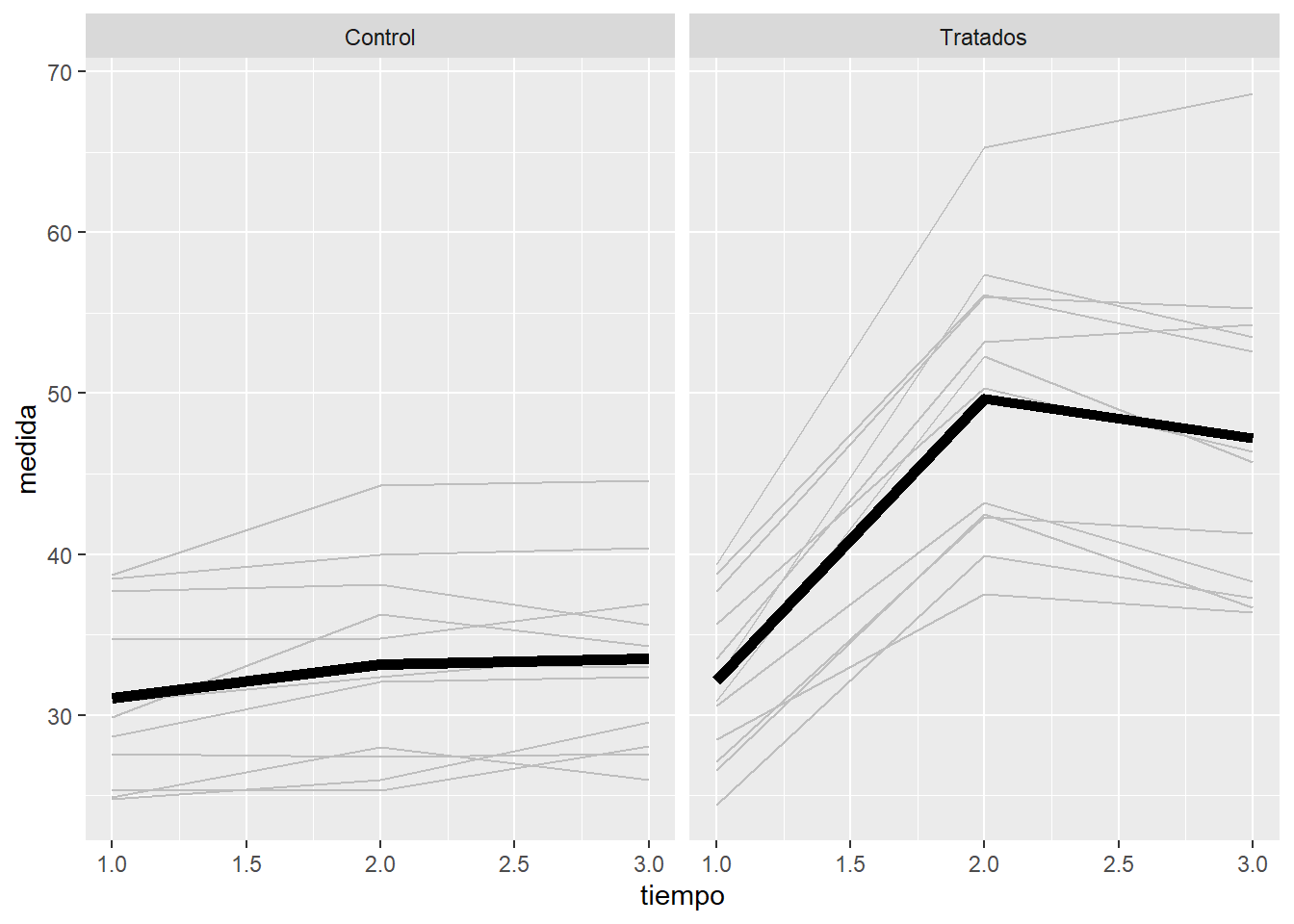

Para trat=1, la medida parece que no sube o sube muy poco. Mientras que para trat=2 sube mucho hasta la segunda medida y se estabiliza en la tercera medida. Por lo tanto, parece que sí hay una interacción entre el tiempo y el grupo de tratamiento.

5.3.2.2 Suma de cuadrados (ANOVA)

Para ajustar este modelo hay que usar los datos en disposición vertical. Como antes hay que convertir las variables tiempo, indiv2 y trat a factor.

library(ez)

datos.ez <- datos
datos.ez$tiempo <- factor(datos.ez$tiempo)
datos.ez$indiv2 <- factor(datos.ez$indiv2)
datos.ez$trat <- factor(datos.ez$trat)

ezANOVA(data=datos.ez, 
        dv=medida, 
        wid=indiv, 
        within=tiempo, 
        between=trat,
        detailed = TRUE)

$ANOVA
       Effect DFn DFd         SSn       SSd         F            p
1 (Intercept)   1  22 102808.4513 2849.9219 793.63083 9.363797e-19
2        trat   1  22   1952.0835 2849.9219  15.06913 8.040878e-04
3      tiempo   2  44   1397.0700  312.7422  98.27755 5.878117e-17
4 trat:tiempo   2  44    811.8211  312.7422  57.10794 5.921847e-13
  p<.05       ges
1     * 0.9701554
2     * 0.3816578
3     * 0.3063929
4     * 0.2042582

$`Mauchly's Test for Sphericity`
       Effect         W           p p<.05
3      tiempo 0.5725954 0.002866835     *
4 trat:tiempo 0.5725954 0.002866835     *

$`Sphericity Corrections`
       Effect       GGe        p[GG] p[GG]<.05       HFe
3      tiempo 0.7005722 1.520842e-12         * 0.7336894
4 trat:tiempo 0.7005722 1.003472e-09         * 0.7336894
         p[HF] p[HF]<.05
3 4.932994e-13         *
4 4.400536e-10         *

Vemos como se aplican las correcciones sólo en los términos “intra sujeto” que son tiempo y la interacción trat:tiempo, ya que el test de Mauchly es significativo (p-valor < 0.05). Una vez aplicados las correcciones sobre los grados de libertad, los p-valores cambian aunque las conclusiones son las mismas: tanto el efecto del tiempo como su interacción con el tratamiento son significativos.

ezPlot(data=datos.ez, 
       dv=medida, 
       wid=indiv, 
       within=tiempo, 
       between=trat,
       x=tiempo,
       split=trat)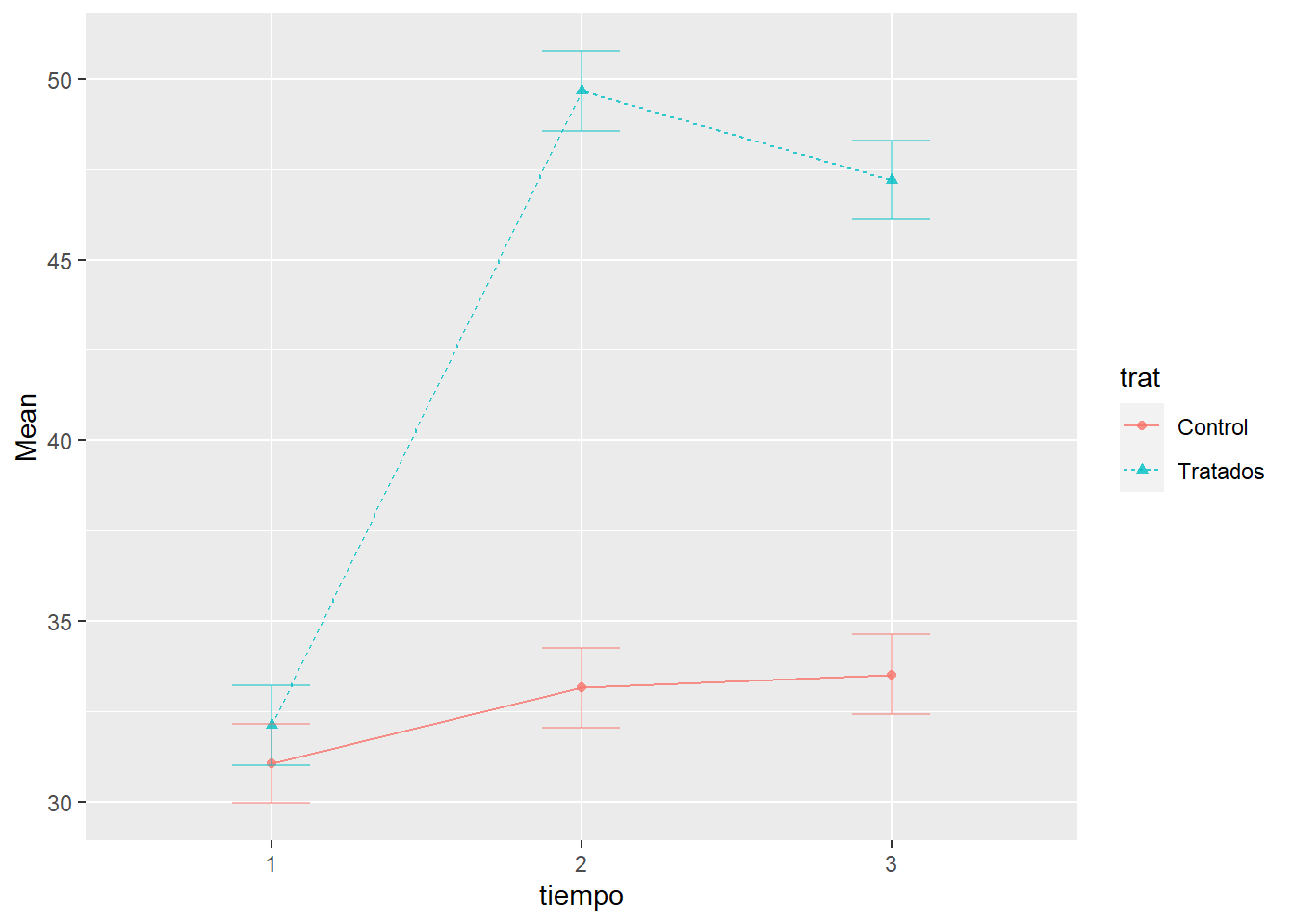

Las conclusiones con la tabla ANOVA corregida (tanto por GG como por HF), se ven claramente en el gráfico de interacción.

5.3.2.3 Modelo de respuesta multivariante (MANOVA)

Para analizar los datos mediante el modelo de respuesta multivariante, como antes hay que disponer los datos de forma horizontal.

datosh <- dcast(datos, indiv + trat ~ paste0("medida_", tiempo),
                 value.var = "medida" )
datosh

   indiv     trat medida_1 medida_2 medida_3
1      1  Control     34.7     34.8     36.9
2      1 Tratados     39.4     65.3     68.6
3      2  Control     38.7     44.3     44.6
4      2 Tratados     33.5     53.2     54.3
5      3  Control     28.7     32.1     32.4
6      3 Tratados     27.1     42.3     41.3
7      4  Control     30.8     32.4     33.8
8      4 Tratados     30.9     52.3     45.7
9      5  Control     29.9     36.3     34.3
10     5 Tratados     32.2     57.4     53.5
11     6  Control     27.6     27.4     27.6
12     6 Tratados     26.6     42.5     36.7
13     7  Control     24.9     28.0     26.0
14     7 Tratados     28.5     37.5     36.4
15     8  Control     37.7     38.1     35.6
16     8 Tratados     37.7     56.0     55.3
17     9  Control     31.0     33.2     33.0
18     9 Tratados     35.7     50.3     46.4
19    10  Control     25.4     25.3     28.1
20    10 Tratados     30.6     43.2     38.3
21    11  Control     24.8     26.0     29.6
22    11 Tratados     24.4     39.9     37.3
23    12  Control     38.5     40.0     40.4
24    12 Tratados     38.8     56.1     52.6

respuesta <- as.matrix(datosh[,c("medida_1","medida_2","medida_3")])
modelo <- lm(respuesta ~ trat, data=datosh)
summary(modelo)

Response medida_1 :

Call:
lm(formula = medida_1 ~ trat, data = datosh)

Residuals:
    Min      1Q  Median      3Q     Max 
-7.7167 -3.9667 -0.7083  4.1271  7.6417 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)    31.058      1.476  21.048 4.57e-16 ***
tratTratados    1.058      2.087   0.507    0.617    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5.112 on 22 degrees of freedom
Multiple R-squared:  0.01156,   Adjusted R-squared:  -0.03337 
F-statistic: 0.2572 on 1 and 22 DF,  p-value: 0.6171


Response medida_2 :

Call:
lm(formula = medida_2 ~ trat, data = datosh)

Residuals:
     Min       1Q   Median       3Q      Max 
-12.1667  -6.6396   0.3375   5.2896  15.6333 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)    33.158      2.113  15.692 1.98e-13 ***
tratTratados   16.508      2.988   5.524 1.50e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 7.32 on 22 degrees of freedom
Multiple R-squared:  0.5811,    Adjusted R-squared:  0.5621 
F-statistic: 30.52 on 1 and 22 DF,  p-value: 1.495e-05


Response medida_3 :

Call:
lm(formula = medida_3 ~ trat, data = datosh)

Residuals:
     Min       1Q   Median       3Q      Max 
-10.8000  -5.9063  -0.6625   5.6250  21.4000 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)    33.525      2.310  14.511 9.55e-13 ***
tratTratados   13.675      3.267   4.186 0.000384 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 8.003 on 22 degrees of freedom
Multiple R-squared:  0.4433,    Adjusted R-squared:  0.418 
F-statistic: 17.52 on 1 and 22 DF,  p-value: 0.0003835

anova(modelo, X=~1)

Analysis of Variance Table


Contrasts orthogonal to
~1

            Df  Pillai approx F num Df den Df    Pr(>F)    
(Intercept)  1 0.88537   81.102      2     21 1.326e-10 ***
trat         1 0.83628   53.633      2     21 5.599e-09 ***
Residuals   22                                             
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Con la instrucción summary, contrasta si la media es diferente entre los dos grupos de tratamiento, y esto lo hace para cada momento por separado.

En la tabla ANOVA, el p-valor de término trat contrasta si el efecto del tiempo es el mismo para los dos tratamientos, o sea, la interacción tratamiento y tiempo, que es lo que nos interesa. Mientras que el término (Intercept) corresponde al efecto marginal del tiempo.

Fíjate qué pasa si no se especifica el argumento X:

anova(modelo)

Analysis of Variance Table

            Df  Pillai approx F num Df den Df    Pr(>F)    
(Intercept)  1 0.97752  289.829      3     20 < 2.2e-16 ***
trat         1 0.84439   36.176      3     20 2.854e-08 ***
Residuals   22                                             
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

En este caso, el p-valor del tratamiento contrasta si hay diferencias entre tratamientos en alguno de los momentos (hay 3 grados de libertad). Y este contraste no es la interacción entre tratamiento y tiempo.

5.3.3 Ejemplo 3

En un estudio se quieren comparar el efecto de régimen de ejercicio sobre el sobrepeso. Para ello se reclutan 100 personas. A la mitad se le asigna el régimen y al resto se le hacen algunas recomendaciones (grupo control). Se mide el índice de masa corporal justo antes de empezar el estudio (momento basal), y al cabo de 1, 2 y 3 semanas. Como la edad es una variable importante para predecir el IMC también se registra.

Los datos los encontrarás en el fichero “imc.csv”

En este ejemplo, vemos como en algunos de los individuos nos falta alguna medida en a partir de la primera semana. Por este motivo usaremos la técnica de los LMM.

datos <- read.csv2("datos/imc.csv")

Nos aseguramos que los datos estén ordenados por individuo y tiempo

datos <- arrange(datos, indiv, tiempo)

Recodificamos nuestra variable tratamiento:

datos$tx <- factor(datos$tx, 1:2, c("Control", "Tratados"))
summary(datos)

   respuesta         indiv            tiempo          edad      
 Min.   : 9.80   Min.   :  1.00   Min.   :0.00   Min.   :25.00  
 1st Qu.:27.02   1st Qu.: 25.75   1st Qu.:0.75   1st Qu.:43.00  
 Median :30.75   Median : 50.50   Median :1.50   Median :49.00  
 Mean   :30.46   Mean   : 50.50   Mean   :1.50   Mean   :49.03  
 3rd Qu.:34.60   3rd Qu.: 75.25   3rd Qu.:2.25   3rd Qu.:57.00  
 Max.   :43.70   Max.   :100.00   Max.   :3.00   Max.   :69.00  
 NA's   :50                                                     
        tx     
 Control :200  
 Tratados:200