11 Análisis discriminante lineal (LDA)

El análisis discriminante lineal (LDA por sus siglas en inglés) es una clasificación de aprendizaje automático supervisado (binario o multimonial) y un método de reducción de dimensiones. LDA encuentra combinaciones lineales de variables que mejor “discriminan” las clases de la variable respuesta.

Un enfoque (Welch) de LDA supone que las variables predictoras son variables aleatorias continuas normalmente distribuidas y con la misma varianza. Para que se cumpla esta condición, normalmente deberemos escalar los datos

Para una variable respuesta de \(k\) niveles, LDA produce \(k-1\) (reglas) discriminantes utilizando el teorema de Bayes.

\[Pr[Y = C_l | X] = \frac{P[Y = C_l] P[X | Y = C_l]}{\sum_{l=1}^C Pr[Y = C_l] Pr[X | Y = C_l]}\]

donde \(Y\) es la variable respuesta, \(X\) son los predictores y \(C_l\) es la clase \(l\)-ésima. Entonces, la probablidad de que \(Y\) sea igual al nivel \(C_l\) dados los predictores \(X\) es igual a la probabilidad a priori de \(Y\) multiplicado por la probabilidad de observar \(X\) si \(Y=C_l\) dividido por la suma de todas las probabilidades de \(X\) data las priors. El valor predicho para cualquier \(X\) es simplemente \(C_l\) que tenga la probabilidad másxima.

Una forma de calcular las probabilidades es asumir que \(X\) tiene una distribución normal multivariante con medias \(\mu_l\) y varianza común \(\Sigma\). Entonces la función de discriminación lineal para el grupo \(l\) es

\[X'\Sigma^{-1}\mu_l - 0.5 \mu_l^{'}\Sigma^{-1}\mu_l + \log(Pr[Y = C_l])\]

La media teórica y la matriz de covarianza se estiman mediante la media muestral \(\mu=\bar{x}_l\) y la covarianza \(\Sigma=S\), y los predictores \(X\) se reemplazan con los predictores de muestra que denotamos \(u\).

Otro enfoque (Fisher) para LDA es encontrar una combinación lineal de predictores que maximice la matriz de covarianza entre grupos, \(B\), relativo a la matriz de covarianza dentro del grupo (intra-grupo) \(W\).

\[\frac{b'Bb}{b'Wb}\]

La solución a este problema de optimización es el vector propio correspondiente al valor propio más grande de \(W^{-1}B\). Este vector es un discriminante lineal (e.g. una variable). Resolver para la configuración para dos grupos la función discriminante \(S^{-1}(\bar{x}_1 - \bar{x}_2)\) donde \(S^{-1}\) es la inversa de la matriz de covarianza de los datos y \(\bar{x}_1\) y \(\bar{x}_2\) son las medias de cada predictor en los grupos de respuesta 1 y 2. En la práctica, una nueva muestra, \(u\) se proyecta sobre la función discriminante como \(uS^{-1}(\bar{x}_1 - \bar{x}_2)\), que devuelve una puntuación discriminante. Luego, una nueva muestra se clasifica en el grupo 1 si la muestra está más cerca de la media del grupo 1 que de la media del grupo 2 en la proyección:

\[\left| b'(u - \bar{x}_1) \right| - \left| b'(u - \bar{x}_2) \right| < 0\] En general, el modelo requiere \(CP + P(P + 1)/2\) parámetros con \(P\) predictores y \(C\) clases. El tener que estimar parámetros extra en los LDA es debido a que el modelo maneja explícitamente las correlaciones entre predictores. Esto debería proporcionar alguna ventaja a LDA sobre la regresión logística cuando hay correlaciones importantes, aunque ambos modelos no serán útiles cuando la multicolinealidad se vuelva extrema.

Take home message:

• La formulación de Fisher es intuitiva, fácil de resolver matemáticamente y, a diferencia del enfoque de Welch, no implica suposiciones sobre las distribuciones subyacentes de los datos.

• En la práctica, es mejor centrar y escalar los predictores y eliminar los predictores de varianza cercana a cero. Si la matriz aún no es invertible, deberíamos usar Penalized Least Squares o Regularización (se verán en otros cursos).

Veamos cómo hacer este análisis para los datos de cáncer de mama vistos en el capítulo anterior. Podemos llevar a cabo los análisis con muchas librerías, aquí usarems MASS. Tal y como es recomendado, usaremos los datos centrados y escalados (e.g normalizados) y eliminados las variables con varianza cercana a 0 que habíamos obtenido con la librería recipes. Usaremos el enfoque de Fisher que es el que más se usa en la actualida y que está implementado en la función lda.

library(MASS)
fit.lda <- lda(diagnosis ~ .,
               data= breast_train_prep)
fit.lda

Call:
lda(diagnosis ~ ., data = breast_train_prep)

Prior probabilities of groups:
        B         M 
0.6265664 0.3734336 

Group means:
  texture_mean  area_mean smoothness_mean compactness_mean symmetry_mean fractal_dimension_mean
B   -0.3345955 -0.5518490       -0.268585       -0.4766017    -0.2791966           -0.004083286
M    0.5614018  0.9259212        0.450646        0.7996673     0.4684507            0.006851150
   texture_se    area_se smoothness_se compactness_se concavity_se `concave points_se` symmetry_se
B  0.01149947 -0.4401372    0.03661085     -0.2657811   -0.2982358          -0.3482647 -0.01040297
M -0.01929442  0.7384853   -0.06142761      0.4459414    0.5003956           0.5843367  0.01745464
  fractal_dimension_se smoothness_worst compactness_worst `concave points_worst` symmetry_worst
B           -0.1039087       -0.3274326         -0.470998             -0.6204192     -0.3412650
M            0.1743434        0.5493836          0.790265              1.0409719      0.5725924
  fractal_dimension_worst
B              -0.2666749
M               0.4474411

Coefficients of linear discriminants:
                                LD1
texture_mean             0.30931136
area_mean                0.68624260
smoothness_mean          0.13601919
compactness_mean        -0.09120911
symmetry_mean           -0.01090323
fractal_dimension_mean  -0.54404616
texture_se               0.03822818
area_se                  0.14461685
smoothness_se            0.33368817
compactness_se          -0.38173259
concavity_se             0.15241639
`concave points_se`      0.22229600
symmetry_se             -0.04340207
fractal_dimension_se    -0.24056708
smoothness_worst        -0.11356764
compactness_worst        0.06356340
`concave points_worst`   0.75475718
symmetry_worst           0.35329884
fractal_dimension_worst  0.83711669

Podemos observar cuánto vale la media para cada variable en cada uno de los grupos, y esto nos puede ayudar a saber qué variables son más importantes. Los coeficientes de los discriminantes lineales también nos pueden ayudar con la interpretación.

Podemos representar el valor de cada grupo para el primer discriminante lineal (sólo hay 1 ya que tenemos 2 grupos).

prd <- predict(fit.lda, breast_train_prep )
ldahist(data = prd$x[,1], g = breast_train_prep$diagnosis)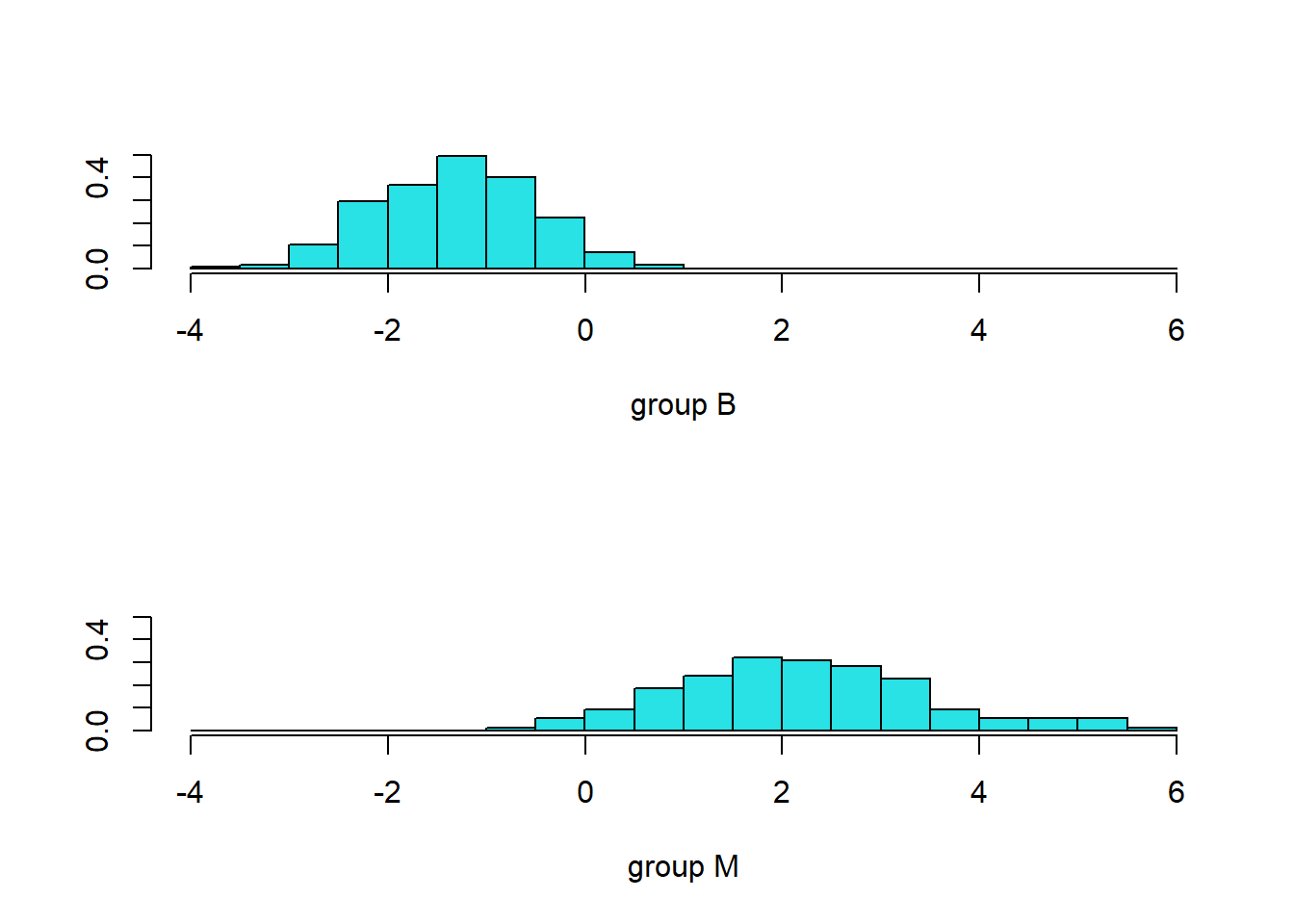

Vemos que los grupos quedan bien separados según el primer discrimiante lineal.

Si tuviéramos 3 grupos también podríamos representar la misma clasificación para el primer y el segundo discriminate lineal. Para ello usaríamos la librería ggord que está en GitHub. Usaremos los datos iris para ilustrar este caso:

# devtools::install_github("fawda123/ggord")
library(ggord)

lnr <- lda(Species~., iris)
ggord(lnr, iris$Species, ylim = c(-5, 5 ))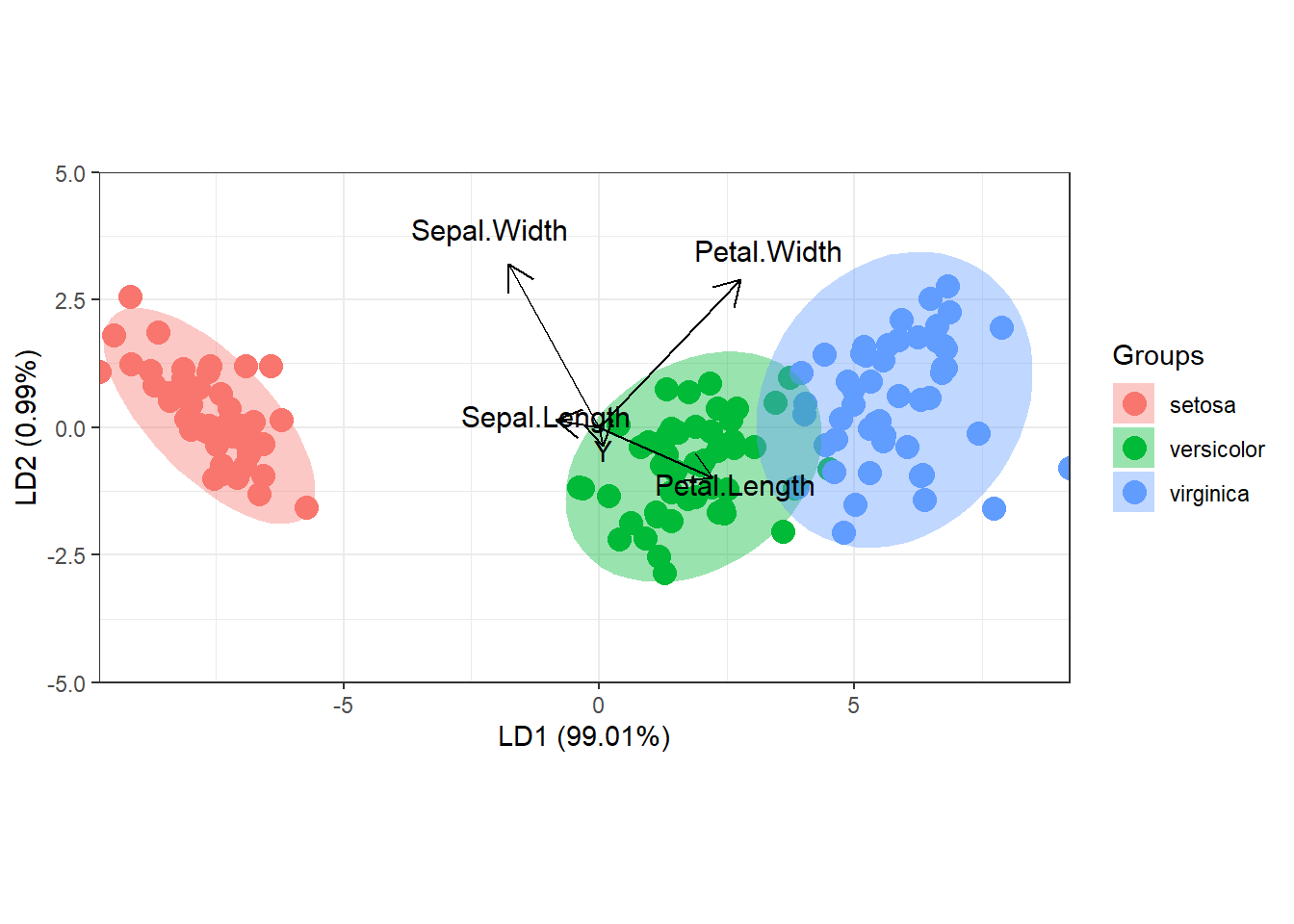

Podemos evaluar de forma manual cómo predice nuestro modelo en la muestra test para nuestro ejemplo de cáncer de mama usando la matriz de confusión:

p.train <- predict(fit.lda, breast_test_prep)$class
tt <- table(predict=p.train, Actual=breast_test_prep$diagnosis)
tt

       Actual
predict   B   M
      B 104   7
      M   3  56

Cuya precisión podemos calcular como:

sum(diag(tt)/sum(tt))

[1] 0.9411765

También podemos evauar la capacidar de nuestro modelo usando, por ejemplo, 10-fold CV con la librería caret. En este caso bastaría con

fitControl <- trainControl(## 10-fold CV
                           method = "repeatedcv",
                           number = 10,
                           ## repeated five times
                           repeats = 5)

train(diagnosis ~ ., 
      data=breast_train_prep,
      method="lda",
      trControl = fitControl)

Linear Discriminant Analysis 

399 samples
 19 predictor
  2 classes: 'B', 'M' 

No pre-processing
Resampling: Cross-Validated (10 fold, repeated 5 times) 
Summary of sample sizes: 359, 359, 359, 359, 359, 359, ... 
Resampling results:

  Accuracy   Kappa    
  0.9593974  0.9106868

Vemos que la precisión estimada en la muestra test es bastante parecida a la predicha mediante 10-fold CV.

EJERCICIO (Entrega en Moodle: P2-LDA):

Implementa una función (idealmente podrímo usar el padigma MapReduce) que nos devuelva la precisión del método LDA usando K-fold CV. Úsa esta función para reproducir los resultados del ejemplo anterior.

11.1 Concurso predicción de actividad física con sensores

El uso de dispositivos portátiles comerciales se está convirtiendo en una herramienta extremadamente útil para medir la actividad física a nivel poblacional. Se han recopilado muchos datos para determinar si estos dispositivos pueden predecir con precisión el estar acostado, sentado y diferentes niveles de intensidad de la actividad física mediante estudios controlados en laboratorios. Tenéis a disposición una base de datos de entrenamiento donde se han recolectado información para 4384 momentos de tiempo en los que los participantes estaban andando en una cinta de correr a distintas intesidades (a su ritmo, 3, 5, y 7 METS) y otros momentos en los que estaban acostados o sentado. Se utilizó calorimetría indirecta para medir el gasto energético. La variable resultado del estudio fua la clase de actividad realizada (variable activity) que tiene estas categorías: Pace walk, Running 3 METs, Running 5 METs, Running 7 METs, Lying y Sitting. Se usaron dos tipos de dispositivos (apple watch y fitbit) para medir distintas variables. Las variables son (a partir de “weight” están medidas con el dispositivo):

 + **id:** Identificador del individuo y momento 
 + **age:** edad
 + **gender:** sexo del individuo
 + **height:** altura del individuo
 + **weight:** peso de individuo
 + **steps:** número de pasos durante la actividad
 + **hear_rate:** pulso durante la actividad
 + **calories:** calorías consumidas en la actividad
 + **distance:** distancia recorrida en la actividad
 + **entropy_heart:** entropía del pulso (la entropía mide la incertidumbre de una fuente de información)
 + **entropy_setps:** entropía del número de pasos en la actividad 
 + **resting_heart:** pulso en reposo
 + **corr_heart_steps:** correlación entre el pulso y los pasos de la actividad
 + **norm_heart:** pulso centrado
 + **intensity_karvonen:** intensidad de la actividad según el índice de Karnoven
 + **sd_norm_heart:** pulso estandarizado
 + **steps_times_distance:** pasos por tiempo y distancia
 + **device:** dispositivo        

TAREA: Debéis crear un modelo predictivo que use todas las variables que hay en el objeto train (obviamente except la variable id) que contiene información para 4384 observaciones, usando la estrategia que creáis oportuna y usando como modelo de aprendijaze o bien KNN o LDA. Podéis hacer todas las cosas que queráis con los datos: estratificarlos, analizarlos todos juntos, usar cualquier método de valización cruzada para validar el modelo, crear nuevas variables, elminar datos, … ya que el objetivo es que apliquéis vuestro modelo a los datos test que contiene la misma información para 1880 observaciones excepto el tipo de actividad que se estaba realizando y que es lo que debéis predecir.

ENTREGA: Debeis subir un fichero NIU.txt (NIU es vuestro identificador de la UAB) a la tarea que hay en Moodle llamada P-Concurso_Predicción con vuestras predicciones para la muestra test. Este fichero debe ser un fichero de texto delimitado por tabulaciones con dos columnas que se llamen “id” y “activity”. Obviamente la columna “id” corresponde a la variable id de la base de datos test y la otra columna debe contener vuestra predicción que debe ser un valor entre: Pace walk, Running 3 METs, Running 5 METs, Running 7 METs, Lying o Sitting. Este fichero se puede crear a partir de un objeto de R que tenga un data.frame con esas dos variables y usando la función write.table() y el argumento `sep=“. También debéis subir el archivo de R (con comentarios) o un R Markdown explicando la estrategia llevada a cabo en la tarea de Moodle llamada P-Concurso_Estrategia.

EVALUACIÓN: Yo evaluaré la capacidad predictiva de vuestro modelo ya que tengo el valor real para esa predicción que habéis hecho y a la cuál no tenéis acceso. La nota con la que os evaluaré esta práctica estará en función de vuestra capacidad de predicción y que básicamente será una nota que estableceré según el ranking obtenido por cada uno de vosotros.

ACCESO A DATOS: Los datos están en un fichero llamado actividad_fisica.Rdata que contiene los objectos train y test a los que he hecho referencia y que están en la carpeta datos del Moodle de la asignatura.

MUY IMPORTANTE: Aquel alumno que me entrege un fichero que no siga el formato indicado, tendrá un 4 en esta práctica como nota máxima.